Ułamki zwykłe na osi liczbowej
Każdemu ułamkowi odpowiada pewien punkt na osi liczbowej, trzeba go tylko znaleźć. W przypadku, gdy chcemy zaznaczyć jeden ułamek, sytuacja jest prosta, dzielimy odcinek jednostkowy na tyle części, ile wskazuje mianownik i odliczamy tyle części, ile wskazuje licznik.
Ułamek $\frac{7}{10}$ jest większy od $0$ i mniejszy od $1$. Odcinek jednostkowy $[0, 1]$ dzielimy na dziesięć równych części.
Siódmy punkt podziału będzie odpowiadał ułamkowi $\frac{7}{10}$ na osi liczbowej.
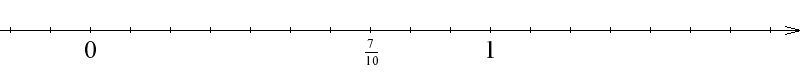
Ułamek $\frac{7}{5}$ to ułamek równy $1\frac{2}{5}$. Znajduje się więc między $1$ a $2$. Odcinek jednostkowy $[1, 2]$ dzielimy na pięć
równych części. Drugi punkt podziału będzie odpowiadał ułamkowi $\frac{7}{5}$ na osi liczbowej.
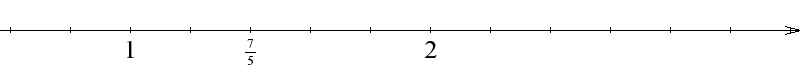
Sytuacja jest trochę trudniejsza, gdy chcemy na jednej osi zaznaczyć więcej niż jeden ułamek, a przy tym część ułamków lub każdy z nich ma inny mianownik. W takiej sytuacji należy najpierw sprowadzić wszystkie ułamki do wspólnego mianownika. Odcinki jednostkowe osi dzielimy na tyle części, ile wskazuje wspólny mianownik i zaznaczamy kolejno ułamki wykorzystując liczniki rozszerzonych ułamków. Czasami istnieje praktyczny problem podziału odcinka jednostkowego, bo może to być niemały wspólny mianownik. Wówczas lepiej uporządkować ułamki rosnąco i szacunkowo zaznaczyć je na możliwej do narysowania osi liczbowej.
Przykład
Zaznacz na osi liczbowej ułamki $\frac{2}{3}, \frac{3}{4}, \frac{7}{6}, \frac{3}{8}, \frac{1}{2}, \frac{1}{12}$.
Ułamki sprowadzamy do wspólnego mianownika, najmniejszym wspólnym mianownikiem jest $24$.
$\frac{2}{3} = \frac{16}{24}$
$\frac{3}{4} = \frac{18}{24}$
$\frac{7}{6} = 1\frac{4}{24}$
$\frac{3}{8} = \frac{9}{24}$
$\frac{1}{2} = \frac{12}{24}$
$\frac{1}{12} = \frac{2}{24}$

Odcinki jednostkowe dzielimy na $24$ równe części. I tak $16$-ty punkt odpowiada ułamkowi $\frac{2}{3}$,
$18$-ty punkt odpowiada ułamkowi $\frac{3}{4}$,
$4$-ty punkt odcinka jednostkowego $[1, 2]$ odpowiada ułamkowi $\frac{7}{6}$,
$9$-ty punkt odpowiada ułamkowi $\frac{3}{8}$, $12$-ty punkt odpowiada ułamkowi $\frac{1}{2}$, a
drugi punkt odpowiada ułamkowi $\frac{1}{12}$.