Wyznacznik macierzy

Teorię wyznaczników zapoczątkował problem znalezienia ogólnego wzoru na rozwiązanie układu n równań liniowych o n niewiadomych. Wzory te zostały podane w XVIII wieku przez Cramera. Teoria wyznaczników została rozwinięta w XIX wieku, zwłaszcza w pracach Laplace'a, Cauchy'ego i Jacobiego.

Wyznacznik macierzy to funkcja określona na macierzach kwadratowych związana z mnożeniem i dodawaniem odpowiednich elementów danej macierzy tak, by otrzymać pojedynczą liczbę. Inaczej mówiąc wyznacznik macierzy jest to liczba rzeczywista przyporządkowana macierzy kwadratowej. Wyznacznik oznaczamy symbolicznie detA lub |A|.

Niech będzie dana macierz kwadratowa A stopnia n.

Wyznacznikiem nazywamy, takie odwzorowanie, które danej macierzy A = _n×n przyporządkowuje dokładnie jedną liczbę rzeczywistą detA.

Jeśli macierz jest stopnia n = 1, to jej wyznacznik detA = a₁₁.
Jeśli stopień macierzy jest większy niż 1, to jej wyznacznik obliczamy według następującego wzoru:
detA = $\overset{n}{\sum_{i = 1}} {(- 1)}^{i + j} a_{i j} \det M_{i j}$ ,
gdzie detM_ij oznacza wyznacznik macierzy powstałej z macierzy A przez skreślenie i-tego wiersza i j-tej kolumny.

Wartość wyznacznika macierzy _n×n, możemy obliczyć ze wzoru:
detA = ∑ sgn(i₁, i₂, ..., i_n) a_i₁1a_i₂2...a_{i_nn} ,
gdzie sumowanie rozciąga się na wszystkie permutacje (i₁, i₂, ..., i_n) zbioru {1, 2, ..., n}.

W iloczynie a_i₁1a_i₂2...a _{i_nn} występuje dokładnie jeden czynnik z każdego wiersza, mianowicie element a_i₁1 z pierwszego wiersza, z drugiego wiersza element a_i₂2 itd. Ponieważ sumowanie rozciąga się na wszystkie permutacje zbioru {1, 2, ..., n}, więc każda z liczb występuje raz i tylko raz. Oznacza to, że w iloczynie a_i₁1a_i₂2...a _{i_nn} występuje dokładnie jeden czynnik z każdej kolumny.
Dodajemy teraz wszystkie wyrażenia utworzone dla wszystkich permutacji i otrzymujemy pewną liczbę. W ten sposób została określona funkcja, która macierzom kwadratowym przypisuje liczby zwane wyznacznikiem macierzy.
Ponieważ istnieje n! (n silnia) permutacji n elementów, więc podana definicja określa wyznacznik macierzy stopnia n jako sumę n! składników.

Z definicji wynikają bezpośrednio następujące rozwinięcia wyznaczników stopnia drugiego i trzeciego

dla n = 2 $| \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix} | = a_{11} a_{22} - a_{21} a_{12}$

dla n = 3 $| \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix} | = a_{11} a_{22} a_{33} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} - a_{11} a_{23} a_{32} - a_{12} a_{21} a_{33} - a_{13} a_{22} a_{31}$

Dla n = 3 istnieje dokładnie 3! = 6 permutacji, a mianowicie
123, 231, 312, 132, 213, 321
Wypisanym sześciu permutacjom odpowiada sześć składników:
+ a₁₁a₂₂a₃₃, + a₁₂a₂₃a₃₁, + a₁₃a₂₁a₃₂, - a₁₁a₂₃a₃₂, - a₁₂a₂₁a₃₃, - a₁₃a₂₂a₃₁,
Dodając te wyrazy otrzymujemy powyższy wzór.

Istnieje prosty sposób mnemotechniczny zapamiętywania budowy wyznaczników stopnia 3, zwany regułą Sarrusa. Dopisujemy z prawej strony raz jeszcze pierwszą i drugą kolumnę i następnie tworzymy iloczyny ze znakami według następującego schematu:
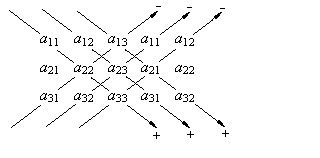
reguła sarrusa

Dla macierzy stopnia czwartego i wyższych obliczanie wyznaczników bezpośrednio z definicji jest na ogół uciążliwe. Wygodnie jest wówczas stosować rozwinięcie Laplace'a.

Macierz kwadratową, której wyznacznik jest równy zero nazywamy macierzą osobliwą, natomiast macierz kwadratową, której wyznacznik jest różny od zera nazywamy macierzą nieosobliwą.

Rozwinięcie Laplace'a
Własności wyznaczników