Egzamin gimnazjalny 2011

Testy matematyczno - przyrodniczy

Informacje do zadań 1 - 3.
Do zespołu szkół, który składa się ze szkoły podstawowej i gimnazjum, uczęszcza 900 uczniów. Chłopcy stanowią 40% uczniów zespołu. 30% uczniów zespołu uczy się w gimnazjum, natomiast 40% uczniów gimnazjum to dziewczęta.

Zadanie 1.
Ilu uczniów uczęszcza do gimnazjum?

A. 630
B. 270
C. 360
D. 540

Rozwiązanie:
30% z 900 = 0,30 · 900 = 270

Zadanie 2.
Ile procent uczniów zespołu szkół stanowią chłopcy uczęszczający do gimnazjum?

A. 12%
B. 18%
C. 45%
D. 24%

Rozwiązanie:
40% uczniów gimnazjum to dziewczęta, zatem chłopcy stanowią 60% uczniów gimnazjum
60% z 270 = 162

\frac{162}{900} \cdot 100 % = 18 %

Zadanie 3.
Ile razy więcej dziewcząt niż chłopców uczy się w tym zespole szkół?
A. 0,5
B. 1,5
C. 3
D. 5

Rozwiązanie:
40% z 900 = 360
60% z 900 = 540

\frac{540}{360} = 1.5

Informacje do zadań 4. i 5.
W wyborach na przewodniczącego samorządu szkolnego kandydowało czworo uczniów. Każdy wyborca oddał jeden ważny głos. Ala otrzymała 25 głosów, a Basia 15 głosów. Na Michała głosowało

\frac{2}{5}

pozostałych osób, a reszta głosów przypadła Oli.

Zadanie 4.
Które wyrażenie przedstawia liczbę osób głosujących na Michała, jeśli w głosowaniu brało udział n osób?

A. $\frac{2}{5} n - 16$
B.

\frac{3}{5} n - 16

\frac{2}{5} n - 40

\frac{3}{5} n - 40

Rozwiązanie:
n - liczba głosujących
Ala: 25 głosów
Basia: 15 głosów
Pozostali: n - 25 - 15 = n - 40
Michał:

\frac{2}{5}

· (n - 40) =

\frac{2}{5} n - 16

Zadanie 5
Kto zajął trzecie miejsce w wyborach, jeśli w głosowaniu wzięło udział 120 osób?
A. Ala
B. Basia
C. Michał
D. Ola

Zadanie 6.
Średnia arytmetyczna pięciu ocen cząstkowych Jacka jest równa 3,4. Jaką średnią ocen będzie miał Jacek, gdy otrzyma jeszcze czwórkę?
A. 4,2
B. 3,7
C. 3,5
D. 3,8

Rozwiązanie:

\frac{5 \cdot 3.4 + 4}{5 + 1} = \frac{21}{6} = 3.5

Zadanie 7.
Miasta wojewódzkie oznaczone numerami od 1 do 4 to

A. 1-Wrocław, 2-Białystok, 3-Poznań, 4-Kielce
B. 1-Poznań, 2-Olsztyn, 3-ŁódĽ, 4-Katowice
C. 1-Bydgoszcz, 2-Olsztyn, 3-Kielce, 4-Opole
D. 1-Poznań, 2-Białystok, 3-ŁódĽ, 4-Wrocław

Zadanie 8.
Na mapie zacieniowano obszary odpowiadające województwom

A. podkarpackiemu i śląskiemu
B. opolskiemu i małopolskiemu
C. dolnośląskiemu i małopolskiemu
D. dolnośląskiemu i podkarpackiemu

Zadanie 9.
W dniach równonocy wiosennej i jesiennej, gdy Słońce nad równikiem góruje w zenicie, oświetla ono

A. bardziej półkulę północną
B. bardziej półkulę południową
C. równomiernie obie półkule
D. tylko obszary okołorównikowe

Zadanie 10.
W ciągu godziny Ziemia obraca się o 15°. Ile czasu zajmuje Ziemi obrót o 110°?

A. 1 godzinę 10 minut
B. 7 godzin 30 minut
C. 4 godziny 40 minut
D. 7 godzin 20 minut

Rozwiązanie:

\frac{110}{15} = 7 \frac{1}{3}

h = 7 h 20 minut

Zadanie 11.
Zjawisko nocy polarnej można zaobserwować na

A. przylądku Horn
B. przylądku Dondra
C. przylądku Morris Jesup
D. Przylądku Południowo-Wschodnim

Zadanie 12.
Dwie identyczne metalowe kulki, z których jedna miała ładunek +10 µC, a druga +2 µC, zetknięto ze sobą, a następnie rozdzielono. Po rozdzieleniu tych kulek każda z nich ma ładunek równy
A. +5 µC
B. +12 µC
C. +8 µC
D. +6 µC

Zadanie 13.
W małym obiegu krew wypływa z prawej komory serca i płynie kolejno:

A. tętnicą płucną, naczyniami włosowatymi płuc, żyłą płucną do lewego przedsionka serca
B. żyłą płucną, naczyniami włosowatymi płuc, tętnicą płucną do prawego przedsionka serca
C. tętnicą płucną, naczyniami włosowatymi płuc, żyłą płucną do prawego przedsionka serca
D. tętnicą płucną, żyłą płucną, naczyniami włosowatymi płuc do lewego przedsionka serca

Zadanie 14.
Aorta (tętnica główna) to naczynie krwionośne, którym płynie krew

A. natlenowana od serca do komórek ciała
B. odtlenowana od serca do komórek ciała
C. natlenowana od komórek ciała do serca
D. odtlenowana od komórek ciała do serca

Zadanie 15.
Zapis uzyskany za pomocą elektrokardiografu, czyli EKG pozwala ocenić

A. poziom cholesterolu we krwi
B. zawartość hemoglobiny we krwi
C. szybkość przepływu krwi w tętnicach i żyłach
D. zmiany, jakie zachodzą w sercu podczas jego pracy

Zadanie 16.
Uczniowie przeprowadzili doświadczenie z siewkami rzodkiewki. Przygotowali trzy zestawy doświadczalne, z których każdy zawierał tę samą liczbę jednakowych siewek. Każdy zestaw siewek naświetlali przez 10 dni światłem o jednakowym natężeniu, ale o innej barwie: białej, czerwonej lub zielonej. Codziennie mierzyli przyrost roślin. Określ problem, który uczniowie chcieli rozwiązać.

A. Czy natężenie światła wpływa na wzrost siewek rzodkiewki?
B. Czy obecność światła wpływa na wzrost siewek rzodkiewki?
C. Czy barwa światła ma wpływ na wzrost siewek rzodkiewki?
D. Czy czas naświetlania ma wpływ na wzrost siewek rzodkiewki?

Zadanie 17.
Komórki bakterii, w przeciwieństwie do komórek organizmów jądrowych, nie mają

A. cytoplazmy
B. mitochondriów
C. rybosomów
D. błony komórkowej

Zadanie 18.
Masa cząsteczkowa etanu C2H6 jest równa

A. 8 u
B. 13 u
C. 30 u
D. 74 u

Zadanie 19.
W jakim stosunku masowym łączy się węgiel z wodorem w etanie?

A. 1:3
B. 1:4
C. 3:1
D. 4:1

Zadanie 20.
Proces rozpadu kwasów, zasad i soli na jony pod wpływem wody to

A. elektroliza
B. dyfuzja
C. dysocjacja
D. dekantacja

Zadanie 21.
Kwas, którego cząsteczka, rozpadając się całkowicie pod wpływem wody, utworzy największą liczbę jonów, to

A. HNO₃
B. H₃PO₄
C. H₂SO₄
D. H₂CO₃

Zadanie 22.
Wodny roztwór KOH znajduje się w probówce

A. I
B. II
C. III
D. IV

Zadanie 23.
Wskaż zdanie prawdziwe.

A. W probówce I pH roztworu ma wartość około 7
B. W probówce II stężenie jonów OH– jest większe niż jonów H+
C. W probówce III odczyn roztworu jest zasadowy
D. W probówkach II i IV znajdują się roztwory o odczynie obojętnym

Zadanie 24.
Która z narysowanych niżej liter alfabetu greckiego ma tylko jedną oś symetrii?

A. Ω - jedna oś symetrii
B. Θ
C. Χ
D. Φ

Zadanie 25.

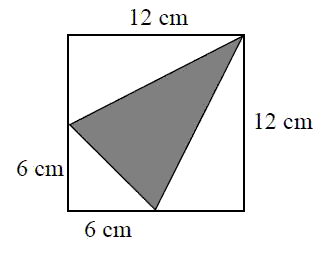
Pole zamalowanego trójkąta jest równe

A. 108 cm²
B. 72 cm²
C. 54 cm²
D. 36 cm²

Rozwiązanie:
Pole kwadratu: 12 · 12 = 144 cm²
Kwadrat podzielony jest na cztery trójkąty, z czego trzy trójkąty prostokątne (niezamalowane).
Pole trójkąta prostokątnego o przyprostokątnych 12 i 6:

\frac{12 \cdot 6}{2} = 36

cm²
Pole najmniejszego trójkąta o przyprostokątnych 6 i 6:

\frac{6 \cdot 6}{2} = 18

cm²

Pole trójkąta zacieniowanego równe jest 144 - 2 · 36 - 18 = 144 - 90 = 54 cm²

Zadanie 26.
Podaj nazwy procesów oznaczonych strzałkami od 1 do 4.

1. fotosynteza
2. odżywianie
3. oddychanie
4. spalanie

Zadanie 27.
Jakie dwie główne grupy destruentów są odpowiedzialne za rozkład martwej materii organicznej?

OdpowiedĽ: bakterie i grzyby

Informacje do zadań 28 - 30
Pewna firma telekomunikacyjna proponuje użytkownikom telefonów komórkowych cztery taryfy: A, B, C, D. Miesięczny rachunek telefoniczny jest sumą kwoty abonamentu i kosztu rozmów według podanych w tabeli stawek.

Taryfa	A	B	C	D
Abonament miesięczny w zł	20	40	80	120
Koszt jednej minuty połączenia w zł	1,10	0,75	0,60	0,40

Zadanie 28.
Pan Kowalski wybrał taryfę C. W marcu otrzymał w promocji 120 bezpłatnych minut. Jaka jest wysokość miesięcznego rachunku telefonicznego, jeśli łączny czas połączeń wykonanych przez pana Kowalskiego w marcu wyniósł 300 minut? Zapisz obliczenia.

Rozwiązanie:
300 min. - 120 min.= 180 minut
80 + 180 · 0,60 = 188 zł

Zadanie 29.
Która z taryf: C czy D jest korzystniejsza, jeżeli miesięczny czas połączeń jest nie mniejszy niż 200 minut? Zapisz obliczenia.

Rozwiązanie:
x - liczba połączeń w minutach
Rozwiązyjemy dwie nierówności:

80 + 0,6x ≥ 120 + 0,4x
0,2x ≥ 40
x ≥ 200

80+0,6x < 120 + 0,4x
0,2x < 40
x < 200

Z pierwszej nierówności wynika, że przy co najmniej 200 połączeniach taryfa D jest korzystniejsza niż taryfa C. Z drugiej nierówności wynika, że taryfa C jest korzystniejsza dla liczby połączeń nie przekraczającej 200.

Odp: Przy co najmniej 200 połączeniach korzystniejsza jest taryfa D.

Zadanie 30.
Ile pełnych minut połączeń można maksymalnie wykonać w ciągu miesiąca, aby rachunek telefoniczny w taryfie A był niższy niż w taryfie B? Zapisz obliczenia.

Rozwiązanie:
x - liczb połączeń w minutach
20 + 1,1x < 40 + 0,75x
0,35x < 20
x<

\frac{400}{7}

57 \frac{1}{7}

57 pełnych minut połączeń do wykorzystania.

Zadanie 31.
W ramce wymieniono przykłady działalności człowieka i jej przyrodnicze uwarunkowania. Uzupełnij tabelę, przyporządkowując właściwe określenia podanym krajom.
tajga, uprawy polderowe, gejzery, winnice, elektrownie geotermalne, obszary depresyjne, klimat śródziemnomorski, pozyskiwanie drewna świerkowego

Lp.	Nazwa kraju	Działalność człowieka	Przyrodnicze uwarunkowania działalności człowieka
1.	Holandia	uprawy polderowe	obszary depresyjne
2.	Islandia	elektrownie geotermalne	gejzery
3.	Włochy	winnice	klimat śródziemnomorski

Informacje do zadań 32 i 33
W celu wyznaczenia oporu elektrycznego opornika Jacek zbudował obwód elektryczny składający się z baterii, opornika, przewodów, amperomierza i woltomierza. Następnie narysował schemat tego obwodu, ale nie wpisał symboli przyrządów pomiarowych.

Zadanie 32.
Uzupełnij schemat obwodu elektrycznego, wpisując właściwe symbole przyrządów.

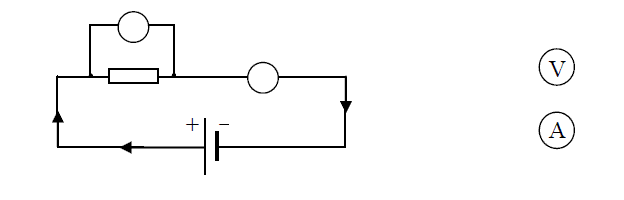
Uzupełnij zdanie, wpisując wielkości fizyczne mierzone tymi przyrządami.
Za pomocą woltomierza Jacek zmierzył napięcie na oporniku, a za pomocą amperomierza natężenie prądu elektrycznego.

Zadanie 33.
Jacek zastąpił baterię w obwodzie dwiema takimi samymi bateriami połączonymi szeregowo. Zauważył wówczas, że napięcie na oporniku wzrosło dwukrotnie.

Uzupełnij zdania
Natężenie prądu elektrycznego wzrosło.
Opór elektryczny opornika nie zmienił się.
Moc opornika wzrosła 4 razy

Zadanie 34.
Uzupełnij tabelę, wpisując odpowiednio nazwy wielkości fizycznych i ich jednostek w układzie SI.

Wielkość fizyczna	Jednostka
Wielkość fizyczna	nazwa	symbol
Praca	dżul	J
Moc	wat	W
Opór	om	Ω
Napięcie elektryczne	wolt	V
Natężenie	amper	A

Zadanie 35.
Ania ulepiła kuliste koraliki o średnicy 1 cm, wykorzystując całkowicie dwa kawałki modeliny. Każdy z kawałków modeliny miał kształt walca o średnicy 2 cm i wysokości 6 cm. Ile koralików ulepiła Ania?

Rozwiązanie:
Obliczamy objętość jednego kawałka modeliny (walec)
r = 1 cm
H = 6 cm
V = πr² · H
V = π · 1 · 6
V = 6π cm³

Ania ma dwa kawałki, zatem objętość wynosi 2 · 6π cm³ = 12π cm³ ≈ 37,69 cm³

Obliczamy objętość jednego koralika (kuli o promieniu 0,5 cm)

V_{k} = \frac{4}{3} π \cdot (\frac{1}{2})^{3} = \frac{π}{6}

cm³ ≈ 0,52 cm³

Z modeliny można ulepić

\frac{12 π}{\frac{π}{6}} = 12 π \cdot \frac{6}{π} = 72

Odp. Ania ulepiła 72 kulki.

Zadanie 36.
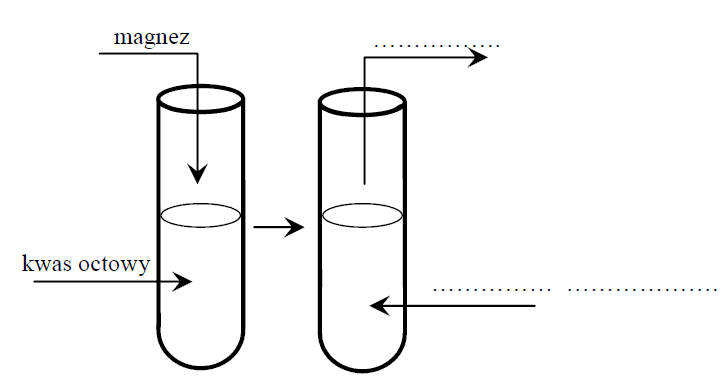
Do roztworu kwasu octowego (CH₃COOH) wsypano wiórki magnezowe (Mg). Otrzymano sól tego kwasu i bezbarwny gaz. W miejscach wskazanych na rysunku wpisz nazwy produktów opisanej reakcji chemicznej i zapisz jej równanie.

Rozwiązanie:
W probówce znajduje się roztwór octanu magnezu, a wydzielający się gaz to wodór
Równanie reakcji: 2CH₃COOH + Mg --> (CH3COO)₂Mg + H₂