Wyra偶enia algebraiczne, zadanie nr 6155
ostatnie wiadomo艣ci | regulamin | latex
| Autor | Zadanie / Rozwi膮zanie |
nice1233 post贸w: 147 |  2018-02-20 11:22:41Uzasadnij, 偶e je艣li wielomian $W(x) = ax^7 + bx^5 + cx^3 + dx + e$ spe艂nia warunek $W(1) = -W(1)$, to 0 jest pierwiastkiem tego wielomianu Wiadomo艣膰 by艂a modyfikowana 2018-02-20 11:31:28 przez nice1233 |
tumor post贸w: 8070 | 2018-02-20 12:29:44 Obawiam si臋, 偶e nie. |
max1233 post贸w: 14 | 2018-02-21 11:14:43 Ten warunek kojarzy mi si臋 z funkcj膮 nieparzyst膮. Czy nie mam racji ? |
max1233 post贸w: 14 | 2018-02-21 11:17:44 A je艣li tak to wiemy 偶e funkcja nieparzysta przechodzi przez punkt (0,0) co automatycznie uzasadnia nam ten warunek. Zgodnie z tymi informacjami umieszczonymi na stronie math.edu.pl Patrz Wiadomo艣膰 by艂a modyfikowana 2018-02-21 11:18:16 przez max1233 |
tumor post贸w: 8070 | 2018-02-21 11:20:03 Je艣li dopuszczamy bardzo odleg艂e skojarzenia. Bardzo. Warunek funkcji nieparzystej wygl膮da艂by $-W(x)=W(-x)$ i rzeczywi艣cie wystarcza艂by dla uzasadnienia, 偶e 0 jest pierwiastkiem wielomianu. Warunek $W(1)=-W(1)$ oznacza tylko, 偶e 1 jest pierwiastkiem wielomianu, nie jest w贸wczas konieczne, by 0 by艂o pierwiastkiem wielomianu. Chyba widzimy r贸偶nice mi臋dzy warunkiem nieparzysto艣ci funkcji a warunkiem z zadania? My艣l臋, 偶e przy braku innego wk艂adu osoba wklejaj膮ca tu zadanie mog艂aby je przynajmniej poprawnie przepisa膰. Wiadomo艣膰 by艂a modyfikowana 2018-02-21 11:21:21 przez tumor |
nice1233 post贸w: 147 | 2018-02-21 11:27:33 Zadanie jest takie same jak w oryginale.  |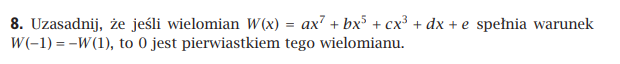
tumor post贸w: 8070 | 2018-02-21 11:29:51 To popatrz jeszcze ze 100 razy, czy takie w艂a艣nie napisa艂e艣 wcze艣niej. |
nice1233 post贸w: 147 | 2018-02-21 11:34:56 Ok.Rozumiem. 殴le przepisa艂em zadanie do zeszytu z podr臋cznika. Przepraszam za roztargnienie. |
tumor post贸w: 8070 | 2018-02-21 11:36:33 Podstaw za x liczb臋 1, wtedy otrzymasz W(1). Jak podstawisz za x liczb臋 -1, otrzymasz W(-1). Je艣li to wstawisz do r贸wnania W(-1)=-W(1), to wyliczysz e=0. A je艣li e=0, to mo偶na wy艂膮czy膰 x przed nawias we wzorze wielomianu. |
| strony: 1 | |
Prawo do pisania przys艂uguje tylko zalogowanym u偶ytkownikom. Zaloguj si臋 lub zarejestruj